基本的な常微分方程式の解き方-1階微分方程式-
概要
微分方程式は 物理学等 の様々な場面で使われている。
今回は、基本的な微分方程式の解法についてまとめた。
- 直接微分形
- 変数分離形
- 同次形
- 1階線形微分方程式
目次
直接微分形
下の形で書ける微分方程式を直接微分形と言う。
この形の方程式は両辺をxで積分することですぐに求めることが出来る。
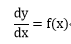 ・・・(1-1)
・・・(1-1)
解法
式1-1の両辺を積分すればよい
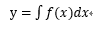
変数分離形
下式のように、右辺がxの関数f(x)とyの関数g(y)の積で書くことが出来る方程式を、変数分離形という。
この形の方程式は、f両辺をf(x)で割ったのち、xで積分する事により求めることが出来る。
この形の方程式は、f両辺をf(x)で割ったのち、xで積分する事により求めることが出来る。
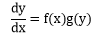 ・・・(2-1)
・・・(2-1)
解法
式2-1の両辺をg(y)で割る
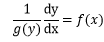 ・・・(2-2)
・・・(2-2)
両辺をxで積分する。
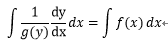 ・・・(2-3)
・・・(2-3)
ここで右辺の積分で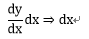 と置き換えられるので式2-3は以下のようになる。
と置き換えられるので式2-3は以下のようになる。
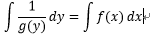 ・・・(2-4)
・・・(2-4)
後は両辺をそれぞれ積分しyを求めればよい。
同次形
右辺がy/xの関数として書ける微分方程式を同次形の微分方程式という。
この式はu=y/xと置くことで、変数分離形の方程式に帰着させることが出来る。
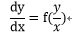 ・・・(3-1)
・・・(3-1)
解法
u=y/xを用いると、式3-1の左辺は次のようになる。
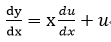 ・・・(3-2)
・・・(3-2)
これとuを式3-1に代入すると、次のようになる。
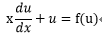 ・・・(3-3)
・・・(3-3)
これを変形すれば変数分離形の方程式(式3-4)が出来る。
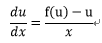 ・・・(3-4)
・・・(3-4)
以降は前節と同じ方法で解くことが出来る。
1階線形微分方程式
1階線微分方程式とは、以下のようにxの関数p(x)とq(x)を用いて書ける方程式である。 この方程式はe (∫p(x)dx) を両辺に掛ける事で解くことが出来る。
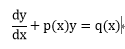 ・・・(4-1)
・・・(4-1)
解法
上式4-1の両辺にe (∫p(x)dx) を掛ける。
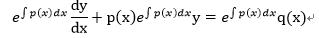 ・・・(4-2)
・・・(4-2)
ここで左辺を変形すると以下のようになる。
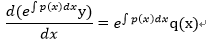 ・・・(4-3)
・・・(4-3)
後は両辺をxで積分しyについて解けばよい。結果は以下のようになる。
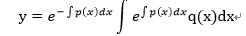 ・・・(4-4)
・・・(4-4)
特にp(x)=α(定数)の場合は以下のようになる。
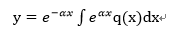 ・・・(4-5)
・・・(4-5)